Sistemas de Coordenadas
Un sistema de coordenadas es un conjunto de valores que permiten definir la posición de cualquier punto de un espacio vectorial. Existen varios tipos de sistemas de coordenadas utilizados para aplicaciones específicas, dentro de ellos se van a describir 3 sistemas usuales en el campo de la ingeniería, estos son:
- Sistema de Coordenadas Cartesianas
- Sistema de Coordenadas Cilíndricas
- Sistema de Coordenadas esféricas
Estos sistemas de coordenadas son de suma importancia ya que para resolver problemas de electrotástica, magnetostática y campos variables en el tiempo, tenemos que tener un conocimiento previo de cómo utilizarlos y cómo hacer cambios de bases vectoriales entre ellos para que la resolución de los problemas sea menos compleja.
Coordenadas Cartesianas
Son un sistema de coordenadas formado por tres planos mutuamente perpendiculares que se cortan en el origen. En el plano, las coordenadas cartesianas o rectangulares x e y se denominan respectivamente abscisa y ordenada.
Para describir la ubicación del punto P en coordenadas cartesianas utilizaremos las siguientes nomenclaturas:

Los factores de escala del sistema de coordenadas cartesiano son:

La expresión de un diferencial de longitud vectorial cartesiano es:

La expresión de los elementos diferenciales de superficie cartesianos es:

El volumen diferencial es el producto cada uno de los escalares de los diferenciales de longitud cartesianos:

En la siguiente imagen se puede observar como se representa un vector de posición en coordenadas cartesianas:

Coordenadas Cilíndricas
Son un sistema de coordenadas utilizado para definir la posición de un punto del espacio mediante un ángulo, una distancia con respecto a un eje y una altura en la dirección del eje. El sistema de coordenadas cilíndricas es muy conveniente utilizarlo en aquellos casos en que se tratan problemas que tienen simetría de tipo cilíndrico o acimutal.
Un punto en coordenadas cilíndricas se representa por 3 variables coordenadas (ρ,φ,z) donde:
ρ: Coordenada radial, definida como la distancia del punto P al eje z, o bien la longitud de la proyección del radiovector sobre el plano XY
φ: Coordenada acimutal, definida como el ángulo que forma con el eje X la proyección del radiovector sobre el plano XY.
z: Coordenada vertical o altura, definida como la distancia, con signo, desde el punto P al plano XY.
Los rangos de variación de las tres coordenadas son:

Una representación gráfica de un vector de posición en coordenadas cilíndricas se puede observar a continuación en la siguiente figura:

A partir del sistema de coordenadas cilíndricas puede definirse una base vectorial en cada punto del espacio, mediante los vectores tangentes a las líneas coordenadas. Esta nueva base puede relacionarse con la base vectorial de las coordenadas cartesianas mediante las siguientes relaciones:



De igual manera se puede relacionar de manera inversa las bases vectoriales cilíndricas y cartesianas de acuerdo a las siguientes relaciones:



Ahora para poder realizar una transformación entre un sistema de coordenadas cartesiano a cilíndrico ó viceversa se deben seguir 2 pasos los cuales se muestran a continuación:
- Transformación de las variables coordenadas
- Transformación de la base vectorial
Para la transformación de las variables coordenadas se deben hacer los cambios entre coordenadas mediante las siguientes relaciones:


Para la transformación de la base vectorial se deben hacer las respectivas proyecciones con las bases vectoriales del sistema de coordenadas hacia el que se quiere llegar, lo cual mediante el siguiente sistema de ecuaciones matricial se resume debido a que es muy largo el mencionado proceso:
Para transformar del sistema de coordenadas cilíndrico al cartesiano:

Y para transformar del sistema de coordenadas cartesiano al cilíndrico:

La expresión de un vector de posición en coordenadas cilíndricas es la siguiente:

Debe notarse que no aparece un término . La dependencia en esta coordenada está oculta en los vectores de la base.
. La dependencia en esta coordenada está oculta en los vectores de la base.
Los factores de escala del sistema de coordenadas cilíndrico son:

La expresión del diferencial de longitud cilíndrico es:

La expresión de los diferenciales de superficie cilíndricos es:

La expresión del diferencial de volumen cilíndrico es:

Coordenadas Esféricas
El sistema de coordenadas esféricas se basa en la misma idea que las coordenadas polares y se utiliza para determinar la posición espacial de un punto mediante una distancia y dos ángulos.
Un punto en coordenadas esféricas se representa al igual que las coordenadas cartesianas y cilíndricas por 3 variables coordenadas (r, θ, φ) donde:
r se le llama radio y es la distancia entre el punto y el origen del sistema de coordenadas cartesiano.
θ (colatitud o ángulo polar ) de 0º a 180º es el ángulo entre el eje z y la línea que une el origen y el punto.
La variable φ es la misma que la del sistema de coordenadas cilíndrico de la cual ya se habló anteriormente.
Los rangos de variación de las tres coordenadas son:

Una representación gráfica de un vector de posición en coordenadas esféricas se puede observar a continuación en la siguiente figura:

Al igual que el sistema de coordenadas cilíndrico, a partir del sistema de coordenadas esféricas puede definirse una base vectorial en cada punto del espacio, mediante los vectores tangentes a las líneas coordenadas. Esta nueva base puede relacionarse con la base fundamental de las coordenadas cartesianas mediante las relaciones:

De igual manera se puede relacionar de manera inversa las bases vectoriales esféricas y cartesianas de acuerdo a las siguientes relaciones:

Para aplicar el proceso de transformación de sistema de coordenadas ya hablado anteriormente, se deben seguir los mismos pasos anteriormente descritos.
Para transformar las variables coordenadas entre los sistemas de coordenadas se deben utilizar las siguientes relaciones:


Para la transformación de la base vectorial las ecuaciones matriciales son las siguientes:
Para transformar del sistema de coordenadas esférico al cartesiano:

Para transformar del sistema de coordenadas cartesiano al esférico:

La expresión de un vector de posición en coordenadas cilíndricas es la siguiente:

Debe notarse también que no aparecen términos en  y
y  . La dependencia en estas coordenadas está oculta en el vector
. La dependencia en estas coordenadas está oculta en el vector  .
.
Los factores de escala del sistema de coordenadas esférico son:

La expresión del diferencial de longitud esférico es:

La expresión de los diferenciales de superficie esféricos es:

La expresión del diferencial de volumen esférico es:

A continuación se muestra un cuadro en el cual se resume todo lo hablado anteriormente acerca de los tres sistemas de coordenadas:
| Sistema de Coordenada | Cartesianas | Cilíndricas | Esféricas |
| Variables Coordenadas |  |  |  |
| Base Vectorial |  |  |  |
| Factores de Escala |  |  |  |
| Diferenciales de Longitud |  |  |  |
| Diferenciales de Superficie |  |  |  |
| Diferenciales de Volumen |  |  |  |


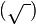 (Fx)2 + (Fy)2
(Fx)2 + (Fy)2 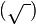 5)2 + (10)2 =
5)2 + (10)2 = 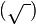 125
125
 DISTANCIA (x) = 38.8 km
DISTANCIA (x) = 38.8 km
















