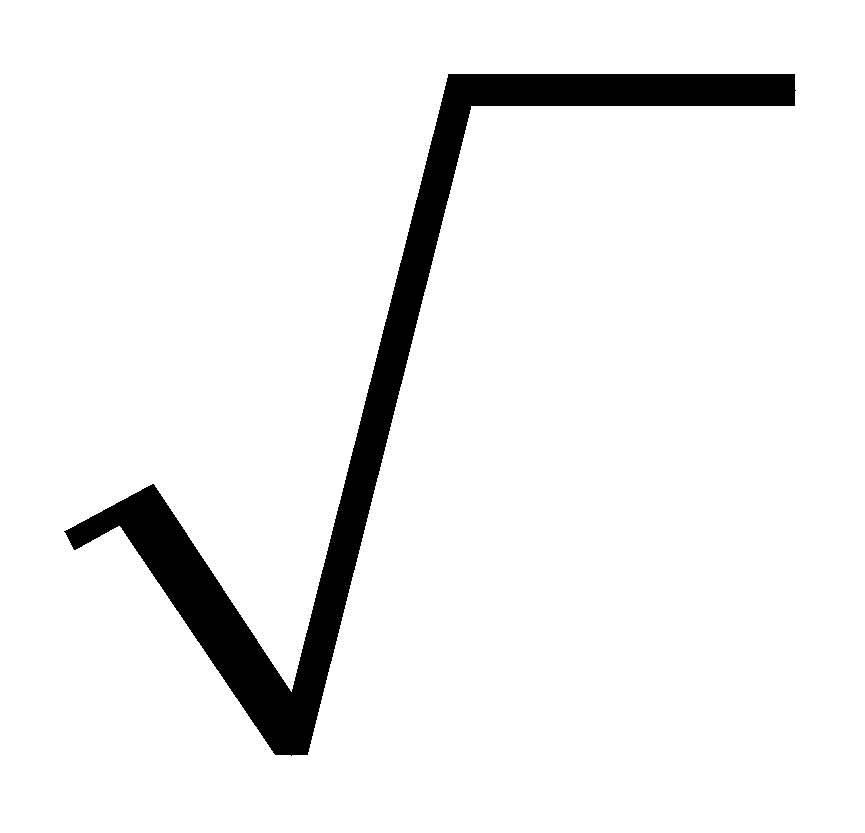FRENAR O ACELERAR

FÍSICA UNIVERITARIO SEARS ZEMANSKY

2.61.- Un auto de 3.5 m viaja con rapidez constante de 20 m/s y se acerca a un cruce de 20 m de ancho. El semáforo se pone en amarillo cuando el frente del aunto está a 50 m del cruce. Si el conductor pisa el freno, el auto se frenará a-3.8 m/s^{2, si pisa el acelerador el auto acelerará a 2.3} m/s^{2.
El semáforo estará en amarillo 3.0 s. Suponga que el conductor reacciona instantáneamente, ¿deberá éste, para no estar en el cruce con el semáforo en rojo, pisar el freno o el acelerador?}

Vcte= 20 m/s
Carretera= 20 m
Cruce = 50 m
Frena =-3.8 m/s^{2
Acelera= 2.3} m/s^{2
Amarillo= 3 s
af=} -3.8 m/s2
a= ^2.3 m/s<sup>2
Δt= 3 s

SUPONIENDO QUE ACELERA, LOGRARÁ EL CRUCE EN 3 s?...</sup>
Δx = 73.5 m
Δt= 3 s

Δx=V0Δt + 1/2 a (Δt)²
=(20)(3)+ 1/2 (2.3)(3)<sup>2

=70.35 m - no pasa (3 s)</sup>

AHORA CALCULAR Δt SUSTITUYENDO EN Δx

73.5 = (20)(Δt) +1/2 (2.3)(Δt)²
20Δt +1/2 2.3Δt²- 73.5= 0

- b ± √b⌃2 + 4ac / 2a
Δt= 3.11 s


FRENA

Δx=V0Δt + 1/2 a (Δt)²
=(20)(3)+ 1/2 (-3.8)(3)²
= 77.1 m - pasa

08/09/'09

Para los vectores A y B de la siguiente figura, use el método de componentes para obtener la magnitud y dirección de
a) A+B
b) suma vectorial de B +A
c) la diferencia vectorial de A-B
d) la diferencia vectorial de B-A














A= <-12,0>
XB= B Cos 37 = 14.37
YB= B Sen 37 = 10.83
B= <14.37,>

a) A+B = B+A= <2.37,> ϕ= 77.65º M= 11.08 m
c) <-12,0> - <14.37,> = <-26.37, -10.83> ϕ=292.32º M= 28.5 m
d) <14.37,> - <-12,0> = <26.37,> ϕ=67.67º M= 28.5

08/09/'09

¿En qué lugar el oficial alcanza el automóvil?

¿En qué tiempo y a qué velocidad?







FÓRMULAS

V = Δx/Δt = x2-x1/t2-t1 = Δx =VΔt
a =ΔV/Δt= Vf-Vi/t2-t1 = ΔV = aΔt

Δx= VoΔt + 1/2 a(Δt)⌃2

DATOS

Va= 15 m/s
a= 3 m/s⌃2
Δx=?
Δt=?
Δp=?

-AUTOMÓVIL (MRU)-
Δx= VoΔt
x0= 0
t0= 0
Vo= 15 m/s = Va
xf=? xa=?
tf= ? ta=?
Vf=?

-OFICIAL (MRUA)-
x0= 0
t0= 0
Vo= 0
xf=xp=? xa=?
tf= tp=? ta=?
Vf=Vp=?

PARA EL AUTOMÓVIL
Δx= xa - x0 = xa
Δt= ta - t0= ta
ΔV= Va -Va=0= a0= 0
xa= Vata
xp= o + 1/2 ap (tp)⌃2 -como xa=xp
Vata=1/2 aptp⌃2
ta=tp
Va=1/2 aptp
tp=ta = 2Va/ap = tp= 2(15)/3 = 10 seg.

DISTANCIA
xa=xp= 15(10)
xa= 150 mts.

VELOCIDAD
a =ΔV/Δt = ap=Vp/tp
por lo tanto,
Vp=aptp= (3)(10)=
Vp= 30 mts.

PLANO INCLINADO- 4/09/'09

SEARS ZAMANSKY

1.6 PLANO INCLINADO

DIAGRAMA CUERPO LIBRE donde ΙΙ: paralelo, ✕: perpendicular



a) ωΙΙ= f ( α, ω)
b) ω✕ = f ( α, ω)

sen α = co/hip = ωΙΙ/ω
ωΙΙ = ω sen α

cos α = ca/ hip = ω✕/ω
ω✕ = ω cos α

c) α = 35º
PΙΙ ≤ 550 N

Pmax = PΙΙ = 550 N
PΙΙ= P sen α
P= PΙΙ/ sen α = 550/ sen 35º =
P= 958 N

COORDENADAS CILÍNDRICAS

COORDENADAS CILÍNDRICAS

r, θ,z de un punto (x, y, z) estan definidas por x= r cos θ, y= r sen θ, z=z.
Para expresar r, θ,z en función de x, y, z y asegurar que θ está entre 0 y 2π podemos escribir
r=√ x²+y²

Halar las coordenadas cilíndricas de (6,6,8)
r=√ x²+y² = √ 6²+6² = 6√2
θ= tan-1 (y/x) = tan-1 (6/6) = 45º

2/09/'09

1.-UNA PARTÍCULA SUFRE 3 DESPLAZAMIENTOS CONSECUTIVOS Δr1 = (1.5i + 3.0j - 1.2k) cm, Δr2 = (2.3i - 1.4j - 3.6k) cm y Δr3 = (-1.3i + 1.5j) cm. HALLAR LAS COMPONENTES DEL VECTOR DESPLAZAMIENTO RESULTANTE Y SU MAGNITUD.

Σvx= (1.5 + 2.3 - 1.3) cm
Σvx= 2.5 cm

Σvy= (3.0 - 1.4 +1.5) cm
Σvy= 3.1 cm

Σvz= (-1.2 - 3.6) cm
Σvz= -4.8 cm

R = √ (2.5)² + (3.1)²+ (-4.8)²
R = 6.23 cm


2.-HALLAR LA SUMA DE DOS VECTORES A y B QUE DESCANZAN SOBRE EL PLANO xy DEFINIDOS COMO SIGUE:
A= 2.00i + 3.00j
B= 5.00i - 4.00j

A+B = <2.00> + <3.00>
A+B = <7.00,>

R= √ (7.00)² + (-1.00)²
R= 7.07
sen θ = co/ hip = 1 / 7.07
θ= Sen⌃-1 (1/7.07)
θ= -8.13
360-8.13= 351.86º
















3.-UNA CARGA DE q1= 7μC SE LOCALIZA EN EL ORIGEN Y UNA CARGA DE q2= -5μC SE UBICA EN EL EJE X A 0.30 m DEL ORIGEN. ENCONTRAR EL CAMPO ELÉCTRICO EN EL PUNTO P, EL CUAL TIENE COORDENADAS (0, 0.4)m


E1 = κ Ιq1Ι / γ2 = (9x10⌃7) (7.0 x 10⌃-6) / (0.4)⌃2

E1= 3.9 x 10⌃5 N/C

E2= 1.8 x 10 ⌃5 N/C






3.1.-EL VECTOR E1 TIENE UNA COMPONENTE Y, EL VECTOR E2 TIENE UNA COMPONENTE X DADA POR E2 Cos θ= 3/5 E2; Y UNA COMPONENTE NEGATIVA -E2 Sen θ= -4/3 E2. POR LO TANTO, E10 3.9x 10⌃5 N/C Y E2=
E2= (1.1x10⌃5i-2.4x10⌃5j)N/C

E= E1 + E2 = 3.9 x10⌃5 N/C + 1.5 x10⌃5 N/C = √ (1.1 x1o⌃5 )² + (1.5 x10⌃5 )²
E= (1.1 x1o⌃5 i + 1.5 x10⌃5 j )
E= 1.8 x10⌃5 N/C
θ= 53.7º

01/ 09/ '09

1.65 SEARS ZEMANSKY pág. 65

|A|= A= 100 N
|B|= B= 80 N
|C|= C= 40 N

¿Cuál es la fuerza resultante R?
R= A + B + C

A = Ax + Ay
B = Bx + By
C = Cx + Cy

R = Ax + Ay - Bx + By - Cx - Cy
R = Axi + Ayj - Bxi + Byj - Cxi - Cyj
R = (Ax-Bx-Cx)i +(Ay+ By- Cy)j

α y β = 30º γ = 53º

sen α = Ay/ A
Ay= A sen α
Ay = 50 N

cos α = Ax/ A
Ax= A cos α
Ax = 86.6 N

sen β = Bx/ B
Bx= B sen β
Bx = 40 N

cos β = By/ B
By= B cos β
By = 69.28 N

sen γ = Cy/ C
Cy = C sen γ
Cy = 31. 94 = 32 N

cos γ = Cx/ C
Cx = C cos γ
Cx = 24.07 N

Σ Vx = (86.6 - 40 - 24.07) N
Σ Vx = 22.53 N

Σ Vy = (50 + 69.28 -32)N
Σ Vy = 87.28 N


R = 22.53 i + 87.28j
R = (22.53)² + (87.28)²
R = 90.14 N

Tan φ = Ry/ Rx
φ = Tan-1 = 72.52º

...............................................................

a = Δv / Δt = Δt = Δv/a
implica

r= r0 + V0 (t- t0)+ 1/2 a (t- t0)²

^{para obtener}

V^{2 =}V0² + 2a Δr

mediante integración

adr = vdv
a ∫ dr = ∫ vdv
a r | r-r0 = v²/v | v-v0
ar- ar0 = 1/2 (v²- v0^{2 )}

2a (r-r0) = v²- v0²

V^{2 =}V0² + 2a Δr

donde Δr = r-r0

COORDENADAS 31/08/'09

P1 (x1, y1)
P2 (x2, y2)


P1P2 =(x2-x1)² + (y2- y1)<sup>2

GRAL..</sup>

y= mx + b m= x2-x1 / y2- y1 ----ANÁLOGO
m= pendiente
b= ordenada al origen

FÍSICA ---


P1 (2,4) P2 (6,8)

P1P2 =16 + 16 = 5.65
..............................
DEMOSTRAR QUE EL TRIÁNGULO ABC CON VÉRTICES EN A (3,3) , B (-3,-3) Y C (-33, 33) ES EQUILÁTERO.



AB = (-6)²+ (-6)² = 8.48
BC = (-3+ 33)² + (-3- 33)² = 8.48
CA = ( 3 + 33)² + (3- 33)²= 8.48
GRAL.....

x²+ y² = r² .....circunferencia

x²- y^{2 = 16.... elipse}

DADAS LAS FÓRMULAS ANTERIORES, ELEGIR UNA Y DESARROLLARLA. ENCONTRAR LOS VALORES DE x, y, RESPECTIVAMENTE.

DE ACUERDO CON LA IMAGEN ANTERIOR SE DESARROLLA LA FÓRMULA DE L CIRCUNFERENCIA: x²+ y² = r^2.
x= r² - y²

X Y

1 3
2 0
3 -5
4 -12
5 -21
6 -32