FISICA II- SANZ GUERRERO NATALIA: REPASO DE TRIGONOMETRÍA

TRIGONOMETRÍA
La parte de las matemáticas que tiene su fundamento en las propiedades especiales del triángulo recto recibe el nombre de trigonometría. Por definición, un triángulo recto es uno que incluye un ángulo de 90º. Considere el triángulo recto de la siguiente figur, donde el lado BC es opuesto al ángulo α, el lado AC es adyascente al ángulo α y el lado AB es la hipotenusa del triángulo.

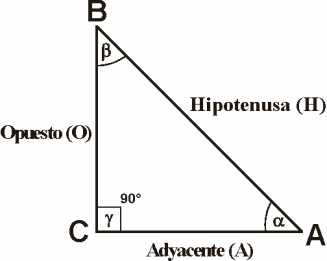
Las tres funciones trigonométricas básicas definidas para dicho triángulo son las funciones seno (sen), coseno (cos) y tangente (tg). En términos del ángulo α estas funciones se definen por medio de:

$\operatorname {sen} \, \alpha= \frac{a}{c} = \frac{\overline{CB}}{\overline{AB}}$ = cateto opuesto (O) / hipotenusa (H)
: $\cos\alpha= \frac{b}{c} = \frac{\overline{AC}}{\overline{AB}}$ = cateto adyascente (A) / hipotenusa (H)

$\tan\alpha= \frac{a}{b} = \frac{\overline{CB}}{\overline{AC}}$ = cateto opuesto (O) / cateto adyascente (A)

El teorema de Pitágoras brinda la siguiente relación entre los lados de un triángulo recto:

$a^2 + b^2 = c^2 \,$

A partir de las definiciones anteriores y del teorema e Pitágoras se deduce que:

$\operatorname {sen}^2 \alpha + \cos^2 \alpha = 1 \,$

$\tan (\alpha) = \frac {\operatorname {sen} (\alpha)}{ \cos (\alpha)}$

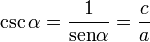
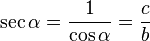
Las funciones cosecante, secante y cotangente están definidas por:: $\csc \alpha = \frac{1}{\operatorname {sen} \alpha} = \frac{c}{a}$; $\sec \alpha = \frac{1}{\cos \alpha} = \frac{c}{b}$

$\cot \alpha = \frac{1}{\tan \alpha} = \frac{b}{a}$
La relaciones siguientes surgen directamente del triángulo recto mostrado anteriormente:: sen α = cos (90º- α)

cos α = sen (90º- α)

cot α = tan (90º- α)

Algunas propiedades de las funciones trigonométricas son:

sen (-α) = -sen α
cos (-α) = cos α
tan (-α) = -tan α

Las siguientes relaciones se aplican a cualquier triángulo:
α + β + γ = 180º

LEY DE COSENOS
a² = b² + c² – 2bc cos α
b² = a² + c² – 2ac cos β
c² = a² + b² – 2ab cos γ

LEY DE SENOS

a/ sen α = b/ sen β = c/ sen γ

ALGUNAS IDENTIDADES TRIGONOMÉTRICAS

$\operatorname{sen}^2\left(x\right)+\cos^2\left(x\right)=1$ csc² α = 1 + cotg² α

$\begin{align} \operatorname{sen} 2\theta &= 2 \operatorname{sen} \theta \cos \theta \ \\ &= \frac{2 \tan \theta} {1 + \tan^2 \theta} \end{align}$ sen² θ/2 = 1/2 (1- cos θ): $\begin{align} \cos 2\theta &= \cos^2 \theta - \operatorname{sen}^2 \theta \\ &= 2 \cos^2 \theta - 1 \\ &= 1 - 2 \operatorname{sen}^2 \theta \\ &= \frac{1 - \tan^2 \theta} {1 + \tan^2 \theta} \end{align}$ cos ² θ/2 = 1/2 (1 + cos θ)
$\tan 2\theta = \frac{2 \tan \theta} {1 - \tan^2 \theta}\,$ 1 - cos θ = 2 sen² θ/2