PROBLEMAS EN CLASE
PREGUNTAS
1.- ¿CUÁL ES LA INTENSIDAD DEL CAMPO ELÉCTRICO PRODUCIDO POR UNA CARGA ELÉCTRICA DE 3x 10⌃-7 C A UNA DISTANCIA DE 2M DE SU CENTRO?
2.- LA INTENSIDAD DEL CAMPO ELÉCTRICO EN UNA CIERT REGIÓN ES DE 3x 10⌃6 N/C. ¿CUÁL ES LA MAGNITUD DE LA CARGA QUE EXPERIMENTA UNA FUERZA DE 12N?
3.- UNA CARGA DE 5x 10⌃-6 C SE ENCUENTRA A 0.5 M DE UNA CARGA DE -3x 10⌃-6 C. ¿CUÁL ES LA MAGNITUD DE DE LA FUERZA DE ATRACCIÓN ENTRE LAS CARGAS?
4.- ¿CUÁL ES LA RESISTENCIA DE UN CONDUCTOR POR EL QUE CIRCULA UNA INTENSIDAD DE CORRIENTE DE 6A CUANDO SE CONECTA UN VOLTAJE DE 90V?
5.- UN APARATO ELÉCTRICO TIENE UNA RESISTENCIA DE 5Ω Y DESARROLLA UNA POTENCIA DE 2000W. ¿QUÉ VOLTAJE NECESITA PARA TRABAJAR?
RESPUESTAS
1.- DATOS
E=? E= k q/d⌃2
q= 3x 10⌃-7 = (9x10⌃9)(3x 10⌃-7 )/ (2)⌃2
d= 2 M E= 675 N/C
2.- DATOS
E= 3x 10⌃6 E= F/q
F=12N q= F/E
q=? =(3x 10⌃6)/ 12
q= 4.0x 10⌃6 C
3.- DATOS
q1=5x 10⌃-6, q2= -3x 10⌃-6
r= 0.5 m
F=?
F= kΙ(q1)(q2)Ι/r⌃2
= (9x10⌃9)Ι(5x 10⌃-6) (-3x 10⌃-6)Ι/ (0.5)⌃2
= 5.4x10 ⌃3 N
4.- DATOS
R=? I= R/V
I= 6A R= V/I
V= 90V = 90/6
R= 15Ω
5.- DATOS
V=? P= V⌃2/R
P= 2000W V= √PR
R= 5Ω = √(2000)(5)
V= 1.0x 10⌃2 V
29 oct 2009
13/ OCT/'09
LEY DE OHM Y POTENCIA ELÉCTRICA
La intensidad de corriente eléctrica que circula por un conductor es directamente proporcional al voltaje aplicado en sus extremos e inversamente proporcional a su resistencia.
I = V/R V=IR R= V/I
I= intensidad (Amperes)
V= voltaje (Volts)
R= resistencia (Ohms)
POTENCIA ELÉCTRICA
Es la cantidad de energía que consume un dispositivo eléctrico por unidad de tiempo.
P= V·I P= I⌃2· R P= V⌃2/R
V= voltaje (V)
P= ptencia (W)
I= intensidad (A)
CIRCUITOS
CIRCUITO EN SERIE
• La intensidad de corriente en cada resistencia es la misma
IT= I1=I2=I3=…=In
• La resistencia total del circuito es igual a la suma de toas las resistencias
RT= R1+R2+R3+…+Rn
• La diferencia de potencial total (voltaje) es igual a la suma de diferencias de potenciales de cada resistencia
VT= V1+V2+V3+…+Vn
CIRCUITOS EN PARALELO
Todos los circuitos conectados en paralelo presentan las siguiente característica:
• La intensidad total es igual a la suma de todas las intensidades en cada resistencia
IT= I1+I2+I3+…+In
• La resistencia total se obtiene con la siguiente fórmula:
1/RT = 1/R1 + 1/R2 +1/R3 +…1/Rn
• La diferencia de potencial total (voltaje) es igual al voltaje de cada resistencia
VT= V1=V2=V3=…=Vn
EJERCICIOS
1.- Dos resistencias de 6 y 4 Ω se encuentran conectadas en serie a un voltaje de 120 V. ¿Cuál es la intensidad que circula por las resistencias?
DATOS
I=?
R= 10 Ω
V= 120V
I=V/R
= 120/10
I= 12 A
2.- Tres resistencias de 3, 6 y 4 Ω se conectan en paralelo y una corriente total de 30 A se distribuye entre las 3. ¿Cuál es el voltaje aplicado al circuito?
R= 3, 6 y 4 Ω 1/RT = 1/R1 + 1/R2 +1/R3 +…1/Rn = 1/RT = 1/1/3 + 1/1/6 +1/1/4 = 1/3/4 = 4/3
I= 30 A
V=? V= 40V
3.- El siguiente circuito ilustra a 4 focos iguales conectados a uan batería. Si el filamento del foco 2 se funde,¿Cuál de las siguientes afirmaciones son correctas? a) Sólo encienden los focos 3 y 4
a) Sólo encienden los focos 3 y 4
b) Sólo foco 1
c) Sólo foco 3
d) Sólo focos 1, 3 y 4
4.- Una resistencia 6Ω se conecta en paralelo con otra de 3Ω. ¿Cuál es la resistencia total del circuito?
1/RT= 1+2/6 = 3/6 = 6/3
RT= 2Ω
La intensidad de corriente eléctrica que circula por un conductor es directamente proporcional al voltaje aplicado en sus extremos e inversamente proporcional a su resistencia.
I = V/R V=IR R= V/I
I= intensidad (Amperes)
V= voltaje (Volts)
R= resistencia (Ohms)
POTENCIA ELÉCTRICA
Es la cantidad de energía que consume un dispositivo eléctrico por unidad de tiempo.
P= V·I P= I⌃2· R P= V⌃2/R
V= voltaje (V)
P= ptencia (W)
I= intensidad (A)
CIRCUITOS
CIRCUITO EN SERIE
• La intensidad de corriente en cada resistencia es la misma
IT= I1=I2=I3=…=In
• La resistencia total del circuito es igual a la suma de toas las resistencias
RT= R1+R2+R3+…+Rn
• La diferencia de potencial total (voltaje) es igual a la suma de diferencias de potenciales de cada resistencia
VT= V1+V2+V3+…+Vn
CIRCUITOS EN PARALELO
Todos los circuitos conectados en paralelo presentan las siguiente característica:
• La intensidad total es igual a la suma de todas las intensidades en cada resistencia
IT= I1+I2+I3+…+In
• La resistencia total se obtiene con la siguiente fórmula:
1/RT = 1/R1 + 1/R2 +1/R3 +…1/Rn
• La diferencia de potencial total (voltaje) es igual al voltaje de cada resistencia
VT= V1=V2=V3=…=Vn
EJERCICIOS
1.- Dos resistencias de 6 y 4 Ω se encuentran conectadas en serie a un voltaje de 120 V. ¿Cuál es la intensidad que circula por las resistencias?
DATOS
I=?
R= 10 Ω
V= 120V
I=V/R
= 120/10
I= 12 A
2.- Tres resistencias de 3, 6 y 4 Ω se conectan en paralelo y una corriente total de 30 A se distribuye entre las 3. ¿Cuál es el voltaje aplicado al circuito?
R= 3, 6 y 4 Ω 1/RT = 1/R1 + 1/R2 +1/R3 +…1/Rn = 1/RT = 1/1/3 + 1/1/6 +1/1/4 = 1/3/4 = 4/3
I= 30 A
V=? V= 40V
3.- El siguiente circuito ilustra a 4 focos iguales conectados a uan batería. Si el filamento del foco 2 se funde,¿Cuál de las siguientes afirmaciones son correctas?
 a) Sólo encienden los focos 3 y 4
a) Sólo encienden los focos 3 y 4b) Sólo foco 1
c) Sólo foco 3
d) Sólo focos 1, 3 y 4
4.- Una resistencia 6Ω se conecta en paralelo con otra de 3Ω. ¿Cuál es la resistencia total del circuito?
1/RT= 1+2/6 = 3/6 = 6/3
RT= 2Ω
15 oct 2009
problemas..12/oct/'09
1.- Una carga de 6x10⌃-6 C se introduce en una región donde actúa un campo de fuerza de 0.18N. ¿Cuál es la intensidad del campo eléctrico en esa región?
E= F/q
= (o.18)/ (6x10⌃-6)
E= 3x10⌃4 N/C
2.- El campo eléctrico en una cierta región es de 5x10⌃20 N/C. Calcule la intensidad de F que actúa sobre un electrón inmerso en este campo.
E= F/q
F= 80 N
3.- La intensidad del campo eléctrico en una cierta región es de 3x10⌃6 N/C. ¿Cuál es la magnitud de la carga que experimenta una fuerza de 12 N?
E= F/q
q= F/E
= (12)/ (3x10⌃6)
q= 4.0 x10⌃-6 C
E= F/q
= (o.18)/ (6x10⌃-6)
E= 3x10⌃4 N/C
2.- El campo eléctrico en una cierta región es de 5x10⌃20 N/C. Calcule la intensidad de F que actúa sobre un electrón inmerso en este campo.
E= F/q
F= 80 N
3.- La intensidad del campo eléctrico en una cierta región es de 3x10⌃6 N/C. ¿Cuál es la magnitud de la carga que experimenta una fuerza de 12 N?
E= F/q
q= F/E
= (12)/ (3x10⌃6)
q= 4.0 x10⌃-6 C
LEY DE COULOMB
1.- Obtener la fuerza resultante entre las cargas q1, q2 y q3 mostradas a continuación
DATOS
q1= q3= 5.0μC
q2= -2μC
a= 0.10 m
Encontrar la Fuerza resultante
 D= F3-1 + F3-2
D= F3-1 + F3-2
la magnitud de F3-2 sobre q3
F3-2= k Ιq3Ι Ιq2Ι / a⌃2
= (9x10⌃9) (5.0x10⌃-6) (2.0 x10⌃-6)/ (0.10)⌃2
F3-2= 9.0 N
F3-1= k Ιq3Ι Ιq1Ι / a⌃2
= (9x10⌃9) (5.0x10⌃-6)(5.0x10⌃-6)/ 2(0.10)⌃2
F3-1= 11.25 N
FR=F3-1 + F3-2
= 9.0 +11.25
FR= 20.25 N
2.- El electrón y protón de un átomo de hidrógeno están separados por una distancia en promedio de 5.3x10⌃-11 m. Encuentre la magnitud de la fuerza eléctrica y la fuerza gravitacional entre las partículas
Fe= ke ΙeΙ⌃2/ r⌃2
=ΙeΙ ΙPΙ / r⌃2
=(9x10⌃9) (1.6x10⌃-19)⌃2/ (5.3x10⌃-11)⌃2
Fe= 8.20 x10⌃-8
Fg= G me mP / r⌃2
donde
G= 6.7 x10⌃-11 N·m⌃2
Fg= (6.7 x10⌃-11)(9.10 x10⌃-31)(1.67x10⌃-27)/ (5.3x10⌃-11)⌃2
Fg= 3.624 10⌃-47 N·kg⌃2
DATOS
q1= q3= 5.0μC
q2= -2μC
a= 0.10 m
Encontrar la Fuerza resultante
 D= F3-1 + F3-2
D= F3-1 + F3-2la magnitud de F3-2 sobre q3
F3-2= k Ιq3Ι Ιq2Ι / a⌃2
= (9x10⌃9) (5.0x10⌃-6) (2.0 x10⌃-6)/ (0.10)⌃2
F3-2= 9.0 N
F3-1= k Ιq3Ι Ιq1Ι / a⌃2
= (9x10⌃9) (5.0x10⌃-6)(5.0x10⌃-6)/ 2(0.10)⌃2
F3-1= 11.25 N
FR=F3-1 + F3-2
= 9.0 +11.25
FR= 20.25 N
2.- El electrón y protón de un átomo de hidrógeno están separados por una distancia en promedio de 5.3x10⌃-11 m. Encuentre la magnitud de la fuerza eléctrica y la fuerza gravitacional entre las partículas

Fe= ke ΙeΙ⌃2/ r⌃2
=ΙeΙ ΙPΙ / r⌃2
=(9x10⌃9) (1.6x10⌃-19)⌃2/ (5.3x10⌃-11)⌃2
Fe= 8.20 x10⌃-8
Fg= G me mP / r⌃2
donde
G= 6.7 x10⌃-11 N·m⌃2
Fg= (6.7 x10⌃-11)(9.10 x10⌃-31)(1.67x10⌃-27)/ (5.3x10⌃-11)⌃2
Fg= 3.624 10⌃-47 N·kg⌃2
1.- Una carga de 5x10⌃-6 C se introduce en una región donde actúa un campo de fuerza de 0.04N. ¿Cuál es la intensidad del campo eléctrico en esa región?
E= F/q
= (o.o4)/ (5x10⌃-6)
E= 8x10⌃3 N/C
2.- El campo eléctrico a una distancia d de una carga q es E, si d se reduce a una cuarta parte. ¿Cuál es la nueva magnitud del nuevo campo eléctrico?
E= K q/d⌃2
= K q/(¼ d⌃2)⌃2
16E= K q/d⌃2
3.- La magnitud de campo eléctrico producido por q= 4 x10⌃-9 C a d= 30 cm de su centro es
E= K q/d⌃2
= (9x10⌃9) · (4x10⌃-9)/ (0.3)⌃2=
E= 400 N/C
E= F/q
= (o.o4)/ (5x10⌃-6)
E= 8x10⌃3 N/C
2.- El campo eléctrico a una distancia d de una carga q es E, si d se reduce a una cuarta parte. ¿Cuál es la nueva magnitud del nuevo campo eléctrico?
E= K q/d⌃2
= K q/(¼ d⌃2)⌃2
16E= K q/d⌃2
3.- La magnitud de campo eléctrico producido por q= 4 x10⌃-9 C a d= 30 cm de su centro es
E= K q/d⌃2
= (9x10⌃9) · (4x10⌃-9)/ (0.3)⌃2=
E= 400 N/C
FUERZA ELECTRICA CONTRA FUERZA GRAVITATORIA
Una partícula α es el núcleo de una átomo de helio.
Tiene una masa m= 6.64x10⌃-27 kg y una carga q= +2e= 3.2x10⌃-19 C.
Compare la fuerza de repulsión eléctrica entre dos partículas α con la fuerza de atracción gravitatoria entre ella.
SOLUCIÓN
Identificar la magnitud Fe de la fuerza eléctrica está dada por la ecuación
Fe= 1/ 4πε0 · q⌃2/r⌃2
Identificar la magnitud Fg de la fuerza gravitatoria está dada por la ecuación
Fg= G m⌃2/ r⌃2
Se comparan estas dos magnitudes calculando su proporción
Fe/Fg= 1/ 4πε0G · q⌃2/ m⌃2
Sustituir valores
9. 0x10⌃9 N·m⌃2/ C⌃2 · (3.2x10⌃-19 C) ⌃2 =
------------------------------- ------------------------------
6.67x10⌃-11 N·m⌃2/ kg⌃2 (6.64 x10⌃-27 kg) ⌃2
3.1 x10⌃35 C⌃2/kg⌃2
donde
1/ 4πε0 = 9. 0x10⌃9 N·m⌃2/ C⌃2 ⇐ Coulomb (cte) k
Tiene una masa m= 6.64x10⌃-27 kg y una carga q= +2e= 3.2x10⌃-19 C.
Compare la fuerza de repulsión eléctrica entre dos partículas α con la fuerza de atracción gravitatoria entre ella.
SOLUCIÓN
Identificar la magnitud Fe de la fuerza eléctrica está dada por la ecuación
Fe= 1/ 4πε0 · q⌃2/r⌃2
Identificar la magnitud Fg de la fuerza gravitatoria está dada por la ecuación
Fg= G m⌃2/ r⌃2
Se comparan estas dos magnitudes calculando su proporción
Fe/Fg= 1/ 4πε0G · q⌃2/ m⌃2
Sustituir valores
9. 0x10⌃9 N·m⌃2/ C⌃2 · (3.2x10⌃-19 C) ⌃2 =
------------------------------- ------------------------------
6.67x10⌃-11 N·m⌃2/ kg⌃2 (6.64 x10⌃-27 kg) ⌃2
3.1 x10⌃35 C⌃2/kg⌃2
donde
1/ 4πε0 = 9. 0x10⌃9 N·m⌃2/ C⌃2 ⇐ Coulomb (cte) k
10 oct 2009
CAMPOS EN EL ESPACIO MATERIAL
CORRIENTE DE CONDUCCIÓN Y CORRIENTE DE CONVECCIÓN Corriente de conducción y corriente de Convección • CONDUCCIÓN: Cuando el calor de propaga sin transporte real de la sustancia que forma el sistema, por medio de intercambios energéticos (choques) entre sus partículas integrantes (átomos, moléculas, electrones...) se dice que se ha transmitido por conducción. La cantidad de calor que fluye a través de un cuerpo por conducción depende del tiempo, del área a través de la cual fluye, del gradiente de temperatura y de la clase de material.

donde k es la conductividad térmica del material, A el área normal a la dirección del flujo de calor, t el tiempo y D T/D L es el gradiente de temperatura. El símbolo D T representa la diferencia de temperatura entre dos superficies paralelas distantes entre sí D L .
Existen grandes diferencias de conductividad térmica para distintos materiales. Los gases tienen una conductividad muy pequeña. Igualmente, los líquidos son en general malos conductores. En el caso de los sólidos, la conductividad térmica varía de una forma extraordinaria, desde valores bajísimos, como en el caso de las fibras de amianto, hasta valores muy altos para l caso de los metales. Los materiales fibrosos, como el fieltro o el amianto, son muy malos conductores (buenos aislantes) cuando están secos ; si se humedecen, conducen el calor bastante bien. Una de las dificultades para el uso de estos materiales como aisladores es el mantenerlos secos.
CONDUCCIÓN.- La conducción es el transporte de calor a través de una sustancia y tiene lugar cuando se ponen en contacto dos objetos a diferentes temperaturas. El calor fluye desde el objeto que está a mayor temperatura hasta el que la tiene menor. La conducción continúa hasta que los dos objetos alcanzan a la misma temperatura (equilibrio térmico). Podemos explicarlo si tenemos en cuenta las "colisiones de las moléculas". En la superficie de contacto de los dos objetos las moléculas del objeto que tiene mayor temperatura, que se mueven más deprisa, colisionan con las del objeto que está a menor temperatura, que se mueven más despacio. A medida que colisionan, las moléculas rápidas ceden parte de su energía a las más lentas. Estas a su vez colisionan con otras moléculas contiguas. Este proceso continúa hasta que la energía se extiende a todas las moléculas del objeto que estaba inicialmente a menor temperatura. Finalmente alcanzan todas la misma energía cinética y en consecuencia la misma temperatura. Algunas sustancias conducen el calor mejor que otras. Los sólidos son mejores conductores que los líquidos y éstos mejor que los gases. Los metales son muy buenos conductores del calor, mientras que el aire es un mal conductor.
• CONVECCIÓN: Cuando el calor se transmite por medio de un movimiento real de la materia que forma el sistema se dice que hay una propagación de calor por convección. Un ejemplo son: Los radiadores de agua caliente y las estufas de aire. La transferencia de calor por corrientes de convección en un líquido o en un gas, está asociada con cambios de presión, debidos comúnmente a cambios locales de densidad. Un aumento de temperatura en un fluido va acompañado por un descenso de su densidad. Si aplicamos calor en la base de un recipiente, el fluido, menos denso en esta parte debido al calentamiento, será continuamente desplazado por el fluido más denso de la parte superior. Este movimiento que acompaña a la transmisión del calor se denomina convección libre. Ejemplos clásicos de convección son : el movimiento del viento sobre la tierra, la circulación del aguan en un sistema de calefacción doméstico. Algunas veces las diferencias de presión se producen mecánicamente mediante una bomba o un ventilador ; en tal caso, se dice que la conducción del calor ocurre por convección forzada. En ambos casos, el calor pasa hacia dentro o fuera de la corriente a lo largo del recorrido. El método de las corrientes de convección es uno de los más eficaces de transferencia de calor y debe tenerse en cuenta cuando se diseñe o construya un sistema de aislamiento. Si se dejan en una casa grandes espacios sin paredes, se forman muy fácilmente corrientes de convección, produciéndose pérdidas de calor. Sin embargo, silos espacios se rompen en pequeños recintos, no son posibles las corrientes de convección y las pérdidas de calor por este método son muy pequeñas. Por esta razón, los materiales aislantes usados en las paredes de refrigeradores o en las de las casas son poroso: viruta de corcho, corcho prensado, lana de vidrio u otros materiales similares. Estos, no solamente son malos conductores por sí mismos, sino que dejan además pequeños espacios de aire, que son muy malos conductores y, al mismo tiempo, lo suficientemente pequeños para que no se produzcan corrientes de convección.
CONVECCIÓN.- La convección tiene lugar cuando áreas de fluido caliente (de menor densidad) ascienden hacia las regiones de fluido frío. Cuando ocurre esto, el fluido frío (de mayor densidad) desciende y ocupa el lugar del fluido caliente que ascendió. Este ciclo da lugar a una continua circulación (corrientes convectivas) del calor hacia las regiones frías. En los líquidos y en los gases la convección es la forma más eficiente de transferir calor. En el verano, en una carretera recalentada, se puede ver como asciende de ella el aire caliente formando una columnas oscilantes. También se ve a veces como asciende el aire desde un radiador (el aire caliente sube y el frío baja). En la imagen siguiente se puede ver como un mechero calienta el aire, éste asciende en una corriente convectiva y hace girar la espiral de papel.

El calor calienta el aire y el papel y además de hacer girar la espiral la alarga y llega a tocar la pinza lo que le impide seguir girando.

donde k es la conductividad térmica del material, A el área normal a la dirección del flujo de calor, t el tiempo y D T/D L es el gradiente de temperatura. El símbolo D T representa la diferencia de temperatura entre dos superficies paralelas distantes entre sí D L .
Existen grandes diferencias de conductividad térmica para distintos materiales. Los gases tienen una conductividad muy pequeña. Igualmente, los líquidos son en general malos conductores. En el caso de los sólidos, la conductividad térmica varía de una forma extraordinaria, desde valores bajísimos, como en el caso de las fibras de amianto, hasta valores muy altos para l caso de los metales. Los materiales fibrosos, como el fieltro o el amianto, son muy malos conductores (buenos aislantes) cuando están secos ; si se humedecen, conducen el calor bastante bien. Una de las dificultades para el uso de estos materiales como aisladores es el mantenerlos secos.
CONDUCCIÓN.- La conducción es el transporte de calor a través de una sustancia y tiene lugar cuando se ponen en contacto dos objetos a diferentes temperaturas. El calor fluye desde el objeto que está a mayor temperatura hasta el que la tiene menor. La conducción continúa hasta que los dos objetos alcanzan a la misma temperatura (equilibrio térmico). Podemos explicarlo si tenemos en cuenta las "colisiones de las moléculas". En la superficie de contacto de los dos objetos las moléculas del objeto que tiene mayor temperatura, que se mueven más deprisa, colisionan con las del objeto que está a menor temperatura, que se mueven más despacio. A medida que colisionan, las moléculas rápidas ceden parte de su energía a las más lentas. Estas a su vez colisionan con otras moléculas contiguas. Este proceso continúa hasta que la energía se extiende a todas las moléculas del objeto que estaba inicialmente a menor temperatura. Finalmente alcanzan todas la misma energía cinética y en consecuencia la misma temperatura. Algunas sustancias conducen el calor mejor que otras. Los sólidos son mejores conductores que los líquidos y éstos mejor que los gases. Los metales son muy buenos conductores del calor, mientras que el aire es un mal conductor.
• CONVECCIÓN: Cuando el calor se transmite por medio de un movimiento real de la materia que forma el sistema se dice que hay una propagación de calor por convección. Un ejemplo son: Los radiadores de agua caliente y las estufas de aire. La transferencia de calor por corrientes de convección en un líquido o en un gas, está asociada con cambios de presión, debidos comúnmente a cambios locales de densidad. Un aumento de temperatura en un fluido va acompañado por un descenso de su densidad. Si aplicamos calor en la base de un recipiente, el fluido, menos denso en esta parte debido al calentamiento, será continuamente desplazado por el fluido más denso de la parte superior. Este movimiento que acompaña a la transmisión del calor se denomina convección libre. Ejemplos clásicos de convección son : el movimiento del viento sobre la tierra, la circulación del aguan en un sistema de calefacción doméstico. Algunas veces las diferencias de presión se producen mecánicamente mediante una bomba o un ventilador ; en tal caso, se dice que la conducción del calor ocurre por convección forzada. En ambos casos, el calor pasa hacia dentro o fuera de la corriente a lo largo del recorrido. El método de las corrientes de convección es uno de los más eficaces de transferencia de calor y debe tenerse en cuenta cuando se diseñe o construya un sistema de aislamiento. Si se dejan en una casa grandes espacios sin paredes, se forman muy fácilmente corrientes de convección, produciéndose pérdidas de calor. Sin embargo, silos espacios se rompen en pequeños recintos, no son posibles las corrientes de convección y las pérdidas de calor por este método son muy pequeñas. Por esta razón, los materiales aislantes usados en las paredes de refrigeradores o en las de las casas son poroso: viruta de corcho, corcho prensado, lana de vidrio u otros materiales similares. Estos, no solamente son malos conductores por sí mismos, sino que dejan además pequeños espacios de aire, que son muy malos conductores y, al mismo tiempo, lo suficientemente pequeños para que no se produzcan corrientes de convección.
CONVECCIÓN.- La convección tiene lugar cuando áreas de fluido caliente (de menor densidad) ascienden hacia las regiones de fluido frío. Cuando ocurre esto, el fluido frío (de mayor densidad) desciende y ocupa el lugar del fluido caliente que ascendió. Este ciclo da lugar a una continua circulación (corrientes convectivas) del calor hacia las regiones frías. En los líquidos y en los gases la convección es la forma más eficiente de transferir calor. En el verano, en una carretera recalentada, se puede ver como asciende de ella el aire caliente formando una columnas oscilantes. También se ve a veces como asciende el aire desde un radiador (el aire caliente sube y el frío baja). En la imagen siguiente se puede ver como un mechero calienta el aire, éste asciende en una corriente convectiva y hace girar la espiral de papel.

El calor calienta el aire y el papel y además de hacer girar la espiral la alarga y llega a tocar la pinza lo que le impide seguir girando.
6 oct 2009
CAMPO ELÉCTRICO
UN CAMPO ELÉCTRICO ES UNA REGIÓN QUE RODEA A UNA CARGA ELÉCTRICA. LA MAGNITUD DEL CAMPO ELÉCTRICO PRODUCIDO POR UN CAMPO DE FUERZA F SOBRE UNA CARGA DE PRUEBA q QUE SE OBTIENE CON LA SIGUIENTE FÓRMULA:
E= F/q
donde
F= magnitud del campo de fuerza
q= carga de prueba
E= amgnitud del campo eléctrico
LA MAGNITUD DEL CAMPO ELÉCTRICO PRODUCIDA POR UNA CARGA PUNTUAL q A UNA DISTANCIA d , DE ELLA SE OBTIENE CON LA SIGUIENTE FÓRMULA:
E= k q/d⌃2
E= F/q
donde
F= magnitud del campo de fuerza
q= carga de prueba
E= amgnitud del campo eléctrico
LA MAGNITUD DEL CAMPO ELÉCTRICO PRODUCIDA POR UNA CARGA PUNTUAL q A UNA DISTANCIA d , DE ELLA SE OBTIENE CON LA SIGUIENTE FÓRMULA:
E= k q/d⌃2
1/oct/'09-PROBLEMA EN CLASES-
1.- Una carga de 3 x 10⌃-6 C y otra de -8 x 10⌃-6 C, se encuentran separadas a 2 m de distancia una de la otra. ¿Cuál es la magnitud de la fuerza de atracción entre ellas?
DATOS
q1= 3 x 10⌃-6 C
q2= -8 x 10⌃-6 C
r= 2 m
k= 9 x 10⌃9 N·m⌃2/ C⌃2 --cte. de Coulomb
F=?
F= k Ιq1q2Ι/ r⌃2
F= (9 x 10⌃9) (3 x 10⌃-6)( -8 x 10⌃-6) / (2)⌃2
F= 5.4 x 10⌃-3 N
2.- Dos cargas eléctricas q1 y q2 se encuentran separadas una distancia d y experimentan una fuerza de repulsión de 40N. Si la distancia entre las cargas se duplica, ¿Cuál es la magnitud de la nueva fuerza de repulsión?
F α q/r⌃2 = F/r⌃2 = 40/ (2r)⌃2
F= 10 N
DATOS
q1= 3 x 10⌃-6 C
q2= -8 x 10⌃-6 C
r= 2 m
k= 9 x 10⌃9 N·m⌃2/ C⌃2 --cte. de Coulomb
F=?
F= k Ιq1q2Ι/ r⌃2
F= (9 x 10⌃9) (3 x 10⌃-6)( -8 x 10⌃-6) / (2)⌃2
F= 5.4 x 10⌃-3 N
2.- Dos cargas eléctricas q1 y q2 se encuentran separadas una distancia d y experimentan una fuerza de repulsión de 40N. Si la distancia entre las cargas se duplica, ¿Cuál es la magnitud de la nueva fuerza de repulsión?
F α q/r⌃2 = F/r⌃2 = 40/ (2r)⌃2
F= 10 N
1 oct 2009
EJERCICIOS
Calcular la fuerza de atracción de dos cargas puntuales de 5 C, cuya separación es 1m.
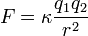
k= 9x10⌃9 N·m⌃2/C⌃2
F= (9x10⌃9)(5)(-5)/ (1)⌃2
F= 2.25x1o⌃11 N
¿Cuál es la distancia de separación de 2 cargas, q1 y q2 de 10 y 15 C que experimenta una fuerza de repulsión de 5x10⌃6 N?
r= √ k q1q2/ F
=√ (9x10⌃9)((10)(15))/ 5x10⌃6
= 519.615 m
¿Qué fuerza experimenta una carga de 5 μC cuya separación es de 2m?
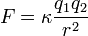 = (9x10⌃9)((5x10⌃-6)(-5x10⌃-6)/ (2)⌃2
= (9x10⌃9)((5x10⌃-6)(-5x10⌃-6)/ (2)⌃2
F= 5.625x10⌃-2 N
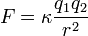
k= 9x10⌃9 N·m⌃2/C⌃2
F= (9x10⌃9)(5)(-5)/ (1)⌃2
F= 2.25x1o⌃11 N
¿Cuál es la distancia de separación de 2 cargas, q1 y q2 de 10 y 15 C que experimenta una fuerza de repulsión de 5x10⌃6 N?
r= √ k q1q2/ F
=√ (9x10⌃9)((10)(15))/ 5x10⌃6
= 519.615 m
¿Qué fuerza experimenta una carga de 5 μC cuya separación es de 2m?
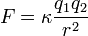 = (9x10⌃9)((5x10⌃-6)(-5x10⌃-6)/ (2)⌃2
= (9x10⌃9)((5x10⌃-6)(-5x10⌃-6)/ (2)⌃2F= 5.625x10⌃-2 N
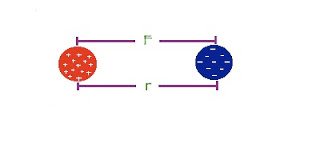
UNIDAD II- ELECTROSTÁTICA
LEY DE COULOMB
La ley de Coulomb puede expresarse como:
La ley de Coulomb puede expresarse como:
- La magnitud de cada una de las fuerzas eléctricas con que interactúan dos cargas puntuales en reposo es directamente proporcional al producto de la magnitud de ambas cargas e inversamente proporcional al cuadrado de la distancia que las separa.
2.64.- EN UNA CARRETERA DE 350 m, EL CORREDOR A PARTE DEL REPOSO Y ACELERA A 1.6m/s⌃2 DURANTE LOS PRIMEROS 30 m Y LUEGO CORRE CON UNA RAPIDEZ CTE. EL CORREDOR B PARTE DEL REPOSO Y ACELERA A DURANTE LOS PRIMEROS 2.0 m/s⌃2 30 m Y DESPUÉS CORRE CON RAPIDEZ CTE. EL CORREDOR COMIENZA A CORRER TAN RÁPIDO COMO INCIA LA COMPETENCIA, PERO AB SE DUERME PRIMERO UNOS MOMENTOS PARA DESCANZAR. ¿CUÁNTO PUEDE DURAR COMO MÁXIMO LA SIESTA DE B PARA QUE NO PIERDA LA CARRERA?
DATOS
Δx1A = 0 + ½ aA (Δt1A)⌃2
30 = ½ (1.6)(Δt1A)2
Δt1A⌃2= 30/ ½(1.6)
Δt1A= √30/ 0.8
Δt1A= 6.12 s
Δx1B = 0 + ½ aB (Δt1B)⌃2
30 = ½ (2.0)(ΔtB)⌃2
ΔtB⌃2= 30/ ½ (2.0)
ΔtB= √ 30
ΔtB= 5.47
V= Δx2/Δt2
VA=V0A +aAΔt1A
=0+(1.6)(6.12)
=9.792 m/s
VB=V0B + aBΔt1B
= 10.94 m/s
Δt= ΔtA + ΔtB
= (6.12 + 35.75) - (31.99 + 5.47)
= 4.4 s
DATOS

Δx1A = 0 + ½ aA (Δt1A)⌃2
30 = ½ (1.6)(Δt1A)2
Δt1A⌃2= 30/ ½(1.6)
Δt1A= √30/ 0.8
Δt1A= 6.12 s
Δx1B = 0 + ½ aB (Δt1B)⌃2
30 = ½ (2.0)(ΔtB)⌃2
ΔtB⌃2= 30/ ½ (2.0)
ΔtB= √ 30
ΔtB= 5.47
V= Δx2/Δt2
VA=V0A +aAΔt1A
=0+(1.6)(6.12)
=9.792 m/s
VB=V0B + aBΔt1B
= 10.94 m/s
Δt= ΔtA + ΔtB
= (6.12 + 35.75) - (31.99 + 5.47)
= 4.4 s
Suscribirse a:
Comentarios (Atom)